Любая линия может быть задана двумя вертексами. Уравнение линии в 3D графике несколько отличается от того, что давали в школе и выглядит так: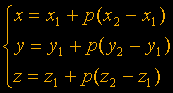

Во-первых, линии могут пересекаться только если они лежат в одной плоскости. Поэтому первым делом нужно проверить выполнение этого условия. Если вы еще не знаете как это делается, узнаете позже, в главе "плоскости". Далее получаем систему из двух систем, каждая из которых содержит по три уравнения. Ого! - подумаете. Нет не ого!: два уравнения, касающиеся оси Z вылетают, т.к уже проверено, что они лежат в одной плоскости => достаточно определить пересечение проекций этих линий на нулевую плоскость. Уже лучше - осталось четыре уравнения. Придется решать 8(. После двух листов упорных вычеслений получаем следующее: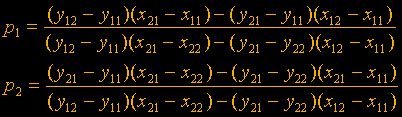

Вероятно, вам еще понадобится знать как опредилить расстояние от любого вертекса до прямой. Я этим никогда не пользовался, но лишним не будет - авось пригодится. Делается это предельно просто. Посмотрим на чертеж. Здесь A и B точки, через которые проходит прямая, а C точка от которой и надо найти расстояние до прямой. Расстояние от точки до прямой - это перпендикуляр, т.е не что иное ка высота CD в треугольнике ABC. Координаты всех точек известны => известны все стороны а по какой-то умной формуле:

где p это полупириметр треугольника ABC.

Вот собственно и все, что нужно знать о линиях. Конечно, нужно уметь находить пересечение линий и плоскостей, но об этом будет рассказано в разделе "плоскости". Я думаю не стоит создавать для линий отдельный класс - это неудобно. Так что просто возьмите кусок кода со всем о чем было сказано в этой главе.